Ganzrationale Funktionen sind Funktionen wie z.B.  y = x³ - 2x² - x + 2

Man nennt diese Funktionen auch Polynomfunktionen, wir benutzen hier aber weiter den Begriff "ganzrationale Funktionen".

Ganz allgemein hat so eine Funktion die Form:

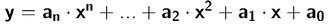
Diese kompliziert aussehende Formel heisst lediglich, dass eine solche Funktion aus einer Reihe von "x hoch Positive Zahl" besteht, mit jeweils einer reelen Zahl davor.

Alle folgenden Funktionen gehören also dazu


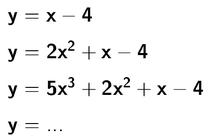
Grad der Funktion:

Die höchste Potenz von x entspricht dem Grad der Funktion.

Die erste Funktion in dem Beispiel oben ist also ersten Grades,

die zweite Funktion im Beispiel hat ein x² und ist deshalb zweiten Grades,

die dritte Funktion wegen dem x³ dritten Grades und so weiter.

 

Nullstellen:

Eine Ganzrationale Funktion kann so viele Nullstellen (also Schnittpunkte mit der x-Achse) haben wie ihr Grad beträgt. Das heißt eine Funktion 3.Grades kann auch maximal drei Nullstellen besitzen.

Um diese Nullstellen zu finden gibt es verschiedene Tricks, wie zum Beispiel:

  • Erraten einer Nullstelle
  • Berechnen mit Polynomdivision
  • Berechnen mit Substitution

Genauer wird das im Kapitel Nullstellen erklärt.

 

 

Graph:

 

 

Der Graph einer ganzrationalen Funktion sieht oft ganz anders als eine Parabel oder eine Gerade aus. Meistens kommt er von links oben oder unten, macht mehrere Kurven und verschwindet wieder nach oben oder unten. Wenn man die Funktion

 

y = x³ - 2x² - x + 2

 

zeichnet erhält man diesen Graphen:

 

Man sieht, dass diese Funktion (3.Grad) 3 mal die x-Achse schneidet, also drei Nullstellen besitzt.