|
Zur Linearfaktorform von quadratischen Funktionen geht es hier! |
Linearfaktorform von ganzrationalen Funktionen:
Man kann eine ganzrationale Funktion nicht nur in der allgemeinen Form
y = x³ - 2x² - x + 2
darstellen, sondern auch als Produkt in der Linearfaktorform:
y = (x + 1) · (x - 1) · (x - 2)
Bei beiden Formen handelt es sich um die gleiche Funktion! Wenn man die Linearfaktorform vollständig ausmultipliziert, dann ist das Ergebnis wieder die allgemeine Form.
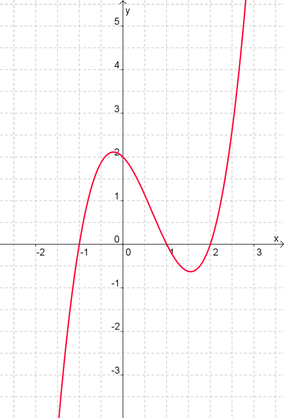
Betrachtet man den Graph der Funktion, kann man an den Schnittstellen mit der x-Achse sofort die einzelnen Linearfaktoren erkennen:
- Der Schnittpunkt bei bei x = -1 entspricht dem Faktor (x + 1)
- Der Schnittpunkt bei bei x = 1 entspricht dem Faktor (x - 1)
- Der Schnittpunkt bei bei x = 2 entspricht dem Faktor (x - 2)
Neben den Linearfaktoren kann die Linearfaktorform auch noch den Leitkoeffizienten a beinhalten, der vor den Faktoren steht.
y = 1 · (x + 1) · (x - 1) · (x - 2)
Der Leitkoeffizient a ist in diesem Beispiel 1.
Um die Linearfaktorform zu bestimmen muss man also folgendes machen:
- Nullstellen bestimmen
- Leitkoeffizient a ablesen
- Alle Faktoren miteinander malnehmen
Aufgabe:
Wir suchen eine ganzrationale Funktion 3.Grades, mit Nullstellen bei x = -2,
x = 0 und x = 1, außerdem soll sie durch den Punkt P (2 / 4) gehen.
Lösung:
Die Nullstellen -2, 0 und 1 können wir direkt in die Linearfaktorform einsetzen:
y = a · (x - (-2)) · (x - 0) · (x - 1)
= a · (x + 2) · x · (x - 1)
Jetzt fehlt uns noch der richtige Leitkoeffizient a, damit die Funktion auch durch den Punkt P verläuft. Dazu setzen wir einfach den Punkt mit x = 2 und y = 4 in die Funktion ein:
4 = a · (2 + 2) · 2 · (2 - 1)
4 = a · 4 · 2 · 1
4 = 8 · a
Also ist a = 0,5
Damit haben wir die komplette Funktion ermittelt:
y = 0,5 · (x + 2) · x · (x - 1)
 FOS-Mathetrainer.de
FOS-Mathetrainer.de