Nullstellen berechnen durch Substitution:

Für bestimmte ganzrationalen Funktionen gibt es auch noch eine andere Methode um die Nullstellen zu berechnen: die Substitution.

Die kann man immer dann verwenden, wenn die Funktion ähnlich wie eine Quadratische Funktion aufgebaut ist, zum Beispiel:

Zum Vergleich die passende Quadratische Funktion:

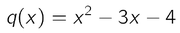
Man sieht, dass die Potenzen von x in der Funktion doppelt so gross sind, also x^4 statt x²  und  x² statt x.

Jetzt verwendet man einen Trick: Man ersetzt einfach die Variable x²  durch einen Platzhalter, der zum Beispiel u heisst. Das nennt man Substitution:

u = x²

Wir setzen also in unsere Funktion f(x) dort, wo x² steht einfach ein u ein: 

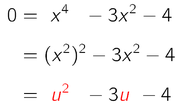
Diese Gleichung können wir wie eine normale quadratische Gleichung für u lösen:

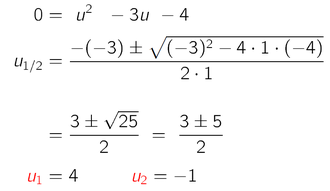
Wir haben also zwei Lösungen für u gefunden: u = 4 und u = -1.

Eigentlich wollen wir aber die Lösungen für x haben, deshalb müssen wir jetzt unseren Platzhalter u in die richtigen Werte für x umrechnen. Das nennt man Resubstitution:

• Resubstitution für u = 4

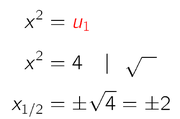
• Resubstitution für u = -1

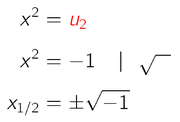
               -> Diese Gleichung hat keine Lösung für x, da -1 keine Wurzel hat!

Wir haben also insgesamt 2 Lösungen für x gefunden: x = 2 und x = -2. Sieht man sich den Graphen der Funktion an, dann sieht man, dass wir richtig gerechnet haben, denn genau in diesen zwei Punkten schneidet der Graph die x-Achse: