Nullstellen mithilfe von "x Ausklammern":
Bei einigen Funktionen lassen sich die Nullstellen ziemlich einfach bestimmen: immer dann, wenn man x Ausklammern kann!
Beispiel:
f(x) = x³ - 2x
Hier steckt in jedem Teil des Funktionsterms mindestens ein x. Wir klammern also zuerst ein x aus:
f(x) = x (x² - 2)
Weil wir Nullstellen suche, suchen wir die Lösung von
x (x² - 2) = 0
Jetzt gibt es zwei Möglichkeiten:
- entweder ist der erste Teil des Produkts ist Null, also x = 0
- oder der zweite Teil des Produkts ist Null, also (x² - 2) = 0
In beiden Fällen hat man eine Nullstelle gefunden. Für den ersten Teil ist klar, die erste Nullstelle liegt bei x1 = 0
Für den zweiten Teil löst man:

Ergebnis: Dank des Ausklammerns von x haben wir sehr schnell die drei Nullstellen gefunden:
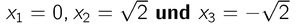
|
Wichtig: Diese Methode funktioniert nur, wenn in jedem Teil des Funktionsterms mindestens ein x steckt! |
Beispiele:
Hier funktioniert die Methode:
f(x) = 5x³ - 4x² - 2x
Hier funktioniert die Methode nicht:
f(x) = x³ - 4x² - 2
Grund: der letzte Teil des Terms (die -2) steht ohne x, also kann man auch kein x Ausklammern!
 FOS-Mathetrainer.de
FOS-Mathetrainer.de