Polynomdivision
Hinter diesem komplizierten Wort versteckt sich ein relativ einfaches Rechenschema.
Dabei teilt man einen längeren Term wie z.B. x² + 2x - 8 (das Polynom) durch einen kurzen Term wie z.B. (x - 2) (den Teiler).
(x² + 2x - 8) : (x - 2) = ???
Man kann das Schema in drei Schritte aufteilen:
- Als erstes teilt man den höchsten Teil des ersten Terms durch den ersten Teil des zweiten Terms und schreibt das Ergebnis hinter das Istgleich:
x² : x = x
- Als zweites nimmt man das Ergebnis vom ersten Schritt mal den ganzen Teiler und schreibt das Ergebnis unter das Polynom:
x · (x - 2) = x² - 2x
- Jetzt macht zieht man das Ergebnis des zweiten Schritts vom Polynom ab und erhält ein Zwischenergebnis:
(x² + 2x - 8) - (x² - 2x) = 4x - 8
- Diese drei Schritte wiederholt man mit dem Zwischenergebnis bis am Ende nur noch eine Zahl als Rest übrigbleit. Im Beispiel ist das die Null
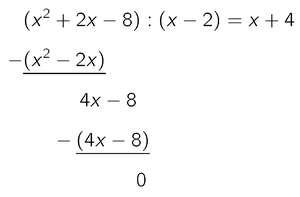
Das Ergebnis unserer Rechnung ist also: x + 4
Zur Kontrolle kann man nachrechnen: (x - 2) · (x + 4) = ...
Wenn jetzt als Ergebnis das ursprüngliche Polynom herauskommt, dann haben wir richtig gerechnet !!!
Übungen:
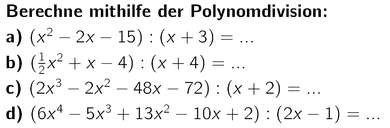
Und für alle, die die Polynomdivision gerne auf musikalischem Weg nochmal wiederholen möchten hier ein super Video aus dem Youtube-Kanal von DorFuchs:
 FOS-Mathetrainer.de
FOS-Mathetrainer.de