Die Wertemenge einer Funktion bezeichnet alle y-Werte, die man erhalten kann, wenn man die erlaubten x-Werte einsetzt.
Um die Wertemenge zu bestimmen braucht man den Scheitelpunkt der Parabel und ihre Öffnungsvariable a. In unserem Beispiel
f (x) = x² - 2x - 3
ist der Scheitelpunkt S (1 / -4) und die Öffnungsvariable a = 1.
Das heißt, die Parabel hat ihren kleinsten y-Wert bei y = -4 und geht ab diesem Wert nach oben.
Die Wertemenge sind also alle y-Werte von -4 bis + Unendlich.
Das sieht in der Intervallschreibweise so aus:
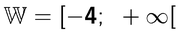
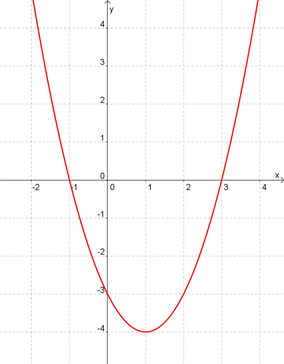
Das sieht man auch sehr gut am Graphen der Funktion: alle y-Werte von -4 bis
+ Unendlich werden durchlaufen.
 FOS-Mathetrainer.de
FOS-Mathetrainer.de